© All rights reserved
Back to top
Article / 03 August 2023

Incircle Sphere Packing: Optimal 3D Sphere Packing on Meshes

Introduction

Hello everyone, I hope you guys reading this are well and happy. Am I obsessed with packing algorithms? Maybe. Will I stop? Probably not :D

In the world of 3D graphics and simulations, efficiently packing spheres onto complex 3D meshes is a common challenge. This task finds applications in computer graphics, gaming, simulations, and virtual environments. Traditionally, the classic circle packing problem has been studied to optimize the arrangement of circles within a 2D container, I actually have an article about it in one of my previous posts and you can check it out here: https://sergicarrion.com/blog/dRvy/generative-circle-packing-patterns-using-houdini-and-unreal. While effective solutions exist for 2D packing, extending this problem to 3D is more intricate due to the complexity of 3D meshes and the need to avoid overlaps.

Inspired by a paper called "Split Packing: An Algorithm for Packing Circles with up to Critical Density", this article explores a triangulate-and-conquer-based algorithm, designed specifically for packing spheres on a 3D mesh. The algorithm allows for the efficient packing of spheres on a 3D mesh while ensuring no overlaps occur between spheres, working with any meshes and without voxelization. 

Alternative Methods for Sphere Packing

When it comes to packing spheres onto a 3D mesh surface, various methods offer different trade-offs between efficiency, accuracy, and control. In this section, we explore several alternative approaches to sphere packing beyond the traditional methods:

  1. Poisson Disk Sampling with Varying Sphere Sizes: Poisson Disk Sampling is a popular technique for generating well-distributed point sets, which can be extended to support spheres of different sizes. By modifying the algorithm to account for sphere radii, this method ensures a minimum distance between sphere centers while offering flexibility in sphere size distribution.
  2. Lloyd's Relaxation and Genetic Algorithms: Lloyd's Relaxation Algorithm and Genetic Algorithms are optimization-based methods that iteratively adjust the sphere positions to achieve a more uniform packing. While effective, they might require more computational resources and may be better suited for smaller-scale packing tasks.
  3. VDB Spheres in Houdini One alternative approach involves converting the mesh to VDB in Houdini and then using VDB Spheres for packing. While this method can be fast, depending on the configuration, it fills the entire mesh with spheres, not just the surface. Cleaning the result and repositioning the spheres close to the surface becomes necessary, making the process more time-consuming. Additionally, this method only works with 3D meshes that can be converted to VDB (closed meshes).
  4. Closest Point Method: This method involves finding the closest points on the mesh surface for each sphere center and placing the sphere there. The process iterates for all spheres until they are packed closely on the mesh.
  5. Apollonian Packing based on Apollonian Gasket Fractal The Apollonian Packing method relies on the Apollonian Gasket fractal to distribute spheres. However, this approach often yields a highly fractal result, providing limited control over the spheres and their radii. As a result, achieving precise and realistic sphere packing may be challenging with this method. While simulations can produce accurate results, they may not be the most efficient option, especially for large-scale 3D meshes.
  6. Particle-Based Methods: These methods treat spheres as particles and simulate their behavior using physics-based simulations. By applying forces between the spheres and the mesh surface, the spheres gradually settle into a stable packing arrangement.
  7. UV Packing: UV packing is another approach that can be used to pack spheres on the surface of a 3D mesh while avoiding overlaps. UV packing involves flattening the 3D mesh onto a 2D plane (UV space) and then performing packing algorithms in 2D. The resulting packed configuration can then be mapped back to the 3D surface. It's versatile, suitable for various mesh types, but requires careful UV unwrapping and additional steps to avoid overlaps when projecting the 2D packing to 3D space.

It's important to note that achieving optimal sphere packing on complex 3D meshes can be a computationally challenging task, and the choice of method may depend on the specific requirements. Additionally, the success of these methods may vary depending on the complexity and shape of the mesh surface and the desired sphere packing density.

The Incircle Sphere Packing Algorithm

By leveraging triangulation and precise incircle calculations, spheres are efficiently placed while avoiding overlaps.

Step 1: Triangulation

The algorithm starts by triangulating the 3D mesh, breaking it down into a collection of triangles. Triangles serve as the basic units for sphere packing, simplifying and speeding up the overall process.

Step 2: Incircle Calculation and 3D Position

For each triangle in the triangulated mesh, the algorithm calculates the incircle and its 3D position for the future sphere placement. The following steps are involved:

  1. Get Triangle Vertices: Obtain the coordinates of the three vertices of the triangle.
  2. Calculate Side Lengths: Determine the length of each side of the triangle using the distance formula.
  3. Calculate Semi perimeter and Area: Compute the semi perimeter (s) and the area (A) of the triangle using the side lengths.
  4. Calculate the Radius of the Incircle: Find the radius (r) of the incircle using the formula A / s.
  5. Calculate 3D Position: Calculate the 3D position (x, y, z) of the incircle.

Step 3: Sphere Instantiation

With the incircle's radius (r) and 3D position (x, y, z) determined, the algorithm instantiates a sphere at each calculated location. As the algorithm progresses through the triangles, spheres are placed in a manner that optimizes the packing while avoiding overlaps.

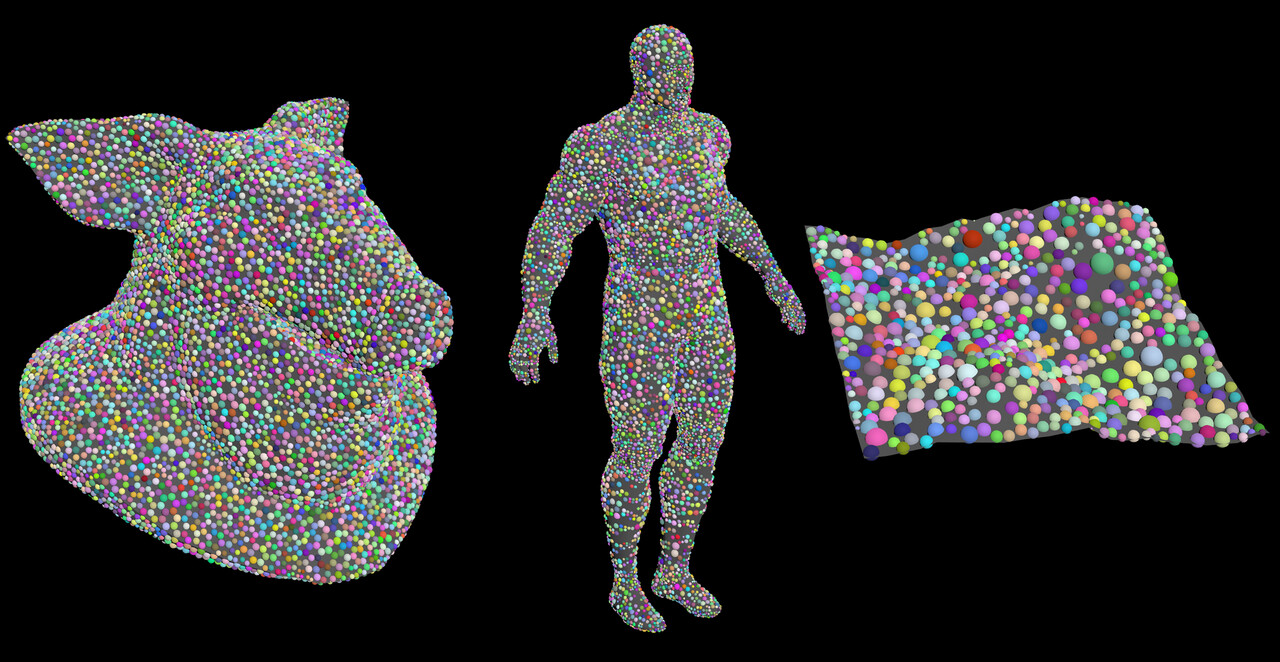
Results

The algorithm's flexibility empowers users to adjust parameters like triangle size and distribution, allowing for diverse arrangements. By customizing triangulation, developers can achieve different packing patterns. 

Complexity

Polycount                Time

036k                        ≈ 01s

150k                        ≈ 03s

300k                        ≈ 08s

600k                        ≈ 16s

2.3 million                ≈ 86s

Based on the statistics above, it appears that the algorithm's time complexity is approximately linear with respect to the number of polygons (polycount) in the mesh. This can be inferred by observing that the execution time roughly increases linearly as the polycount increases. In Big O notation, we can say that the time complexity of the algorithm is O(n), where "n" represents the number of polygons in the mesh.

As for executing the algorithm on the mesh, the execution time will depend on the specific hardware and system specifications of the computer running the algorithm. The provided times are given as approximations and may vary based on the computational resources available. Faster processors, more memory, and optimized implementations can lead to faster execution times. It's important to note that the time complexity (O(n)) focuses on the algorithm's scaling behavior as the polycount grows, while the actual execution time will also be influenced by other factors such as memory access, caching, and threading. 

In my case, this tests were run on the following machine:

OS: Windows 11 Pro

Processor: AMD Ryzen 7 3800X 8-Core Processor                4.10 GHz

RAM: 32.0 GB

GPU: NVIDIA GeForce RTX 2070 SUPER

Conclusion

The algorithm introduced in this article represents an efficient approach to 3D sphere packing on complex meshes. By directly calculating the 3D position of the incircle for each triangle, this algorithm offers versatility, efficiency, and accuracy. 

However, like any algorithm, Incircle Sphere Packing is not without its limitations and challenges. The performance of Split Packing could be impacted by the complexity and quality of the input mesh. The algorithm may have limitations when dealing with extreme triangle size differences, which could lead to suboptimal packing.

Unlike VDB-based packing, which may fill the entire volume and necessitate additional cleaning steps, Split Packing focuses solely on the mesh surface, simplifying the process and ensuring a visually appealing result.

Throughout our exploration of various alternative methods, Incircle Sphere Packing has emerged as a valuable asset for me and I hope for developers working in the realm of 3D and proceduralism. 

Thanks for reading :)!

Update

Since the publication of my article, a research paper titled "Packing Circles and Spheres on Surfaces" (SIGGRAPH 2009) has emerged, providing a more comprehensive exploration of the topic with in-depth insights. Basically a must read if what I explore caught your attention: https://citeseerx.ist.psu.edu/pdf/6af8f2c4d2dc2c04ad6e12b084911076e0448b5c

References

Report